Jak lze měřit bezpečnost? (2. část)

Druhá část článku pokračuje v tématu kvantifikace bezpečnosti. Je vysvětlen vliv matoucích proměnných, především regrese k průměru, dále rozdíl mezi zaznamenanými a očekávanými nehodami. Východiskem je modelování očekávaného počtu nehod v závislosti na intenzitě a dalších charakteristikách.

Článek byl uveřejněn v Silničním obzoru 4/2012.

V první části článku byl popsán tradiční způsob kvantifikace bezpečnosti. Bylo však prokázáno, že každý ukazatel podává jiné výsledky. Jeden z příkladů demonstroval skutečnost, že relativní nehodovost, která se používá nejčastěji, není pro dopravně inženýrské úlohy zcela vhodná.
Jako východisko bylo představeno hodnocení pomocí funkce bezpečnosti. Souvislosti budou popsány v předloženém pokračování článku. Nejprve však bude popsán důležitý jev zvaný regrese k průměru.

1. Regrese k průměru

V první části byly představeny základní ukazatele bezpečnosti. Funkcí ukazatele (indikátoru) je indikovat změny, případně je předvídat. Nárůst nebo pokles hodnoty ukazatele bezpečnosti by tedy mělo indikovat zvýšení nebo snížení bezpečnosti.
Dále bylo uvedeno, že základním ukazatelem, ze kterého se odvozují ostatní ukazatele, je četnost nehod. Navzdory logickým předpokladům, uvedeným v předchozím odstavcích, se její hodnota v čase mění a to i v případě, kdy se nemění žádné kauzální faktory. Náhodné změny četnosti jsou její přirozenou vlastností: jev se nazývá regrese (návrat) k průměru.
Vliv regrese k průměru lze demonstrovat na příkladu. Byla vybrána křižovatka ulic Drobného a Pionýrské v Brně, která dlouhodobě patří mezi nejvíce nehodové [4]. Z údajů Policie ČR (tzv. uzlových sestav) a informací správce komunikací [18] byly zjištěny počty nehod se zraněním v období 1995 – 2010: viz Graf 1. V tomto období nedošlo na křižovatce k žádným stavebním úpravám. Přesto je vidět, že průběh je proměnlivý: po každém výraznějším výkyvu, ať už kladným nebo záporným směrem, následuje regrese k průměru; tento průměr však nelze jednoznačně odhadnout.
Typickou dobou („dlouhodobým“ průměrem), používanou k hodnocení bezpečnosti, jsou 3 roky. V grafu je proto čárkovaně naznačen průběh klouzavého průměru po třech letech. Klouzavý průměr v grafu kolísá mezi hodnotami 1 až 5.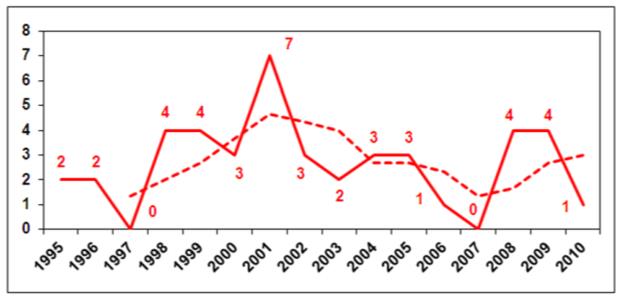

Graf 1 Vývoj počtu nehod se zraněním na křižovatce ulic Drobného a Pionýrské v Brně

Příklad ukazuje vliv náhodného charakteru regrese k průměru a její vliv na zaznamenané četnosti nehod. Tento vliv není ojedinělý ani zanedbatelný. Např. nedávná belgická studie [5] prokázala u vybraných křižovatek, kde nedošlo k žádným změnám, pokles četnosti nehod až o 25 %, který lze přičíst regresi k průměru. Tento vliv mj. zkresluje účinky bezpečnostních opatření: náhodný pokles, způsobený regresí k průměru, je přičítán účinku opatření a účinnost je tak přeceňována. Regrese k průměru dále komplikuje výběr nehodových lokalit: podmínkou výběru nehodové lokality je naplnění výběrového kritéria, definovaného počtem nehod za rok [3, str. 14]. Typicky se volí výběrové kritérium tří osobních nehod za rok; na příkladu výše uvedené křižovatky je zřejmé, že kritérium bude v některých obdobích naplněno a v některých obdobích naopak nenaplněno. Křižovatka se přitom za celé sledované období nezměnila.

Z uvedených skutečností je mj. zřejmé, že účinnost opatření – coby pokles nebo nárůst četnosti nehod – nelze hodnotit prostřednictvím srovnání četnosti nehod před úpravou a po úpravě. Existuje zde několik tzv. matoucích (rušivých) proměnných, které výsledný poměr zkreslují. Regrese k průměru je považována za jednu z nejdůležitějších tzv. matoucích (rušivých) proměnných [9]. Její vliv lze snížit uvážením delšího časového období [13], délka tohoto období však není jednoznačná [14].

Vliv zmíněných matoucích proměnných lze kontrolovat: jedním z řešení je např. uvážení srovnávací skupiny. Komplexní řešení, které eliminuje vliv regrese k průměru i ostatních matoucích proměnných, nabízí tzv. empirická Bayesova metoda, která bude vysvětlena v následujícím textu. Vstupem této metody je tzv. očekávaná četnost, reprezentující dlouhodobý průměr. Bylo dokázáno, že empirická Bayesova metoda tento odhad zpřesňuje a to nejvíce ze všech dostupných metod [8].

Z těchto skutečností vyplývá definice bezpečnosti podle [9]: bezpečnost prvku (místa, úseku, řidiče, vozidla…) je dána očekávaným počtem nehod tohoto prvku za určitou jednotku času.

2. Model nehodovosti

Hodnocení bezpečnosti se tak dostává do sféry tzv. modelování bezpečnosti. Toto téma je v ČR relativně v počátcích. V Centru dopravního výzkumu, v.v.i. jsou v současnosti řešeny dva projekty, které se touto tematikou zabývají:

• VEOBEZ (CG711-078-160) – vývoj modelu bezpečnosti na okružních křižovatkách, představený na  Silniční konferenci 2011 [17],
• IDEKO (VG20112015013)– vývoj modelu bezpečnosti na silnicích II. třídy v extravilánu v Jihomoravském kraji; projekt byl představen v článku [15].

Klíčovým prvkem je zde predikční model nehodovosti. Ten vyjadřuje očekávanou četnost v závislosti na modelovaných veličinách. Tyto tzv. vysvětlující proměnné můžou být různé, v oblasti dopravního inženýrství jsou to však nejčastěji provozní a geometrické charakteristiky komunikací (viz např. přehled dostupných dat [1]).

Jak je z názvu zřejmé, predikční model nehodovosti. Jedná se o variantu funkce bezpečnosti, zmíněné již v první části článku, obecného tvaru: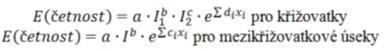                                                        

E(četnost) označuje očekávanou hodnotu četnosti. Základem modelu je již zmíněná funkce bezpečnosti, doplněná o část vyjadřující souhrn vlivu dalších vysvětlujících proměnných.

3. Empirická Bayesova metoda

Podle [10] je cílem empirické Bayesovy metody využití dvou zdrojů informací:

• zaznamenané četnosti nehod,
• očekávané četnosti nehod na podobných místech určené predikčním modelem nehodovosti.

Tyto dva zdroje jsou spojeny pomocí váženého průměru a to následovně [12, str. 16.10]:

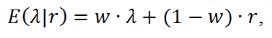
kde λ je očekávaný počet nehod, r je zaznamenaný počet nehod a w je váha, pro kterou platí

                                       

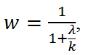
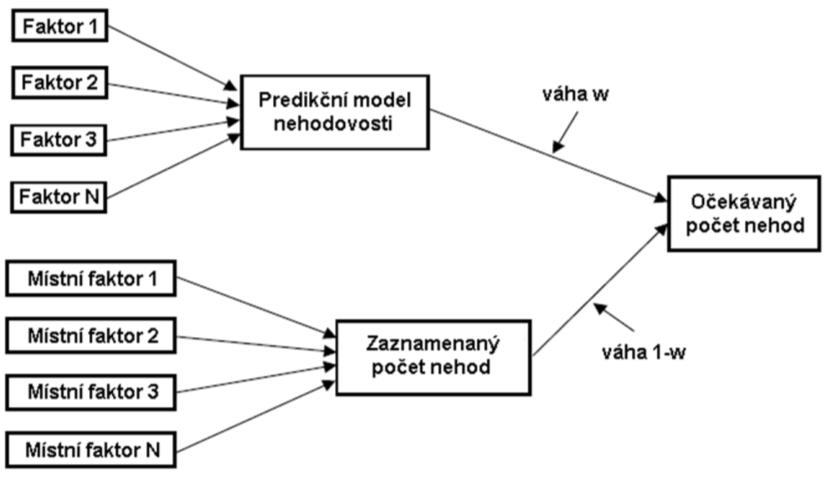
kde k je převrácená hodnota disperzního parametru funkce bezpečnosti predikčního modelu. Výpočet je schematicky znázorněn na Obr. 1, který zároveň vystihuje modelovou definici nehodové lokality [15]: je to místo, které

•     má vyšší očekávaný počet nehod
•     než ostatní podobné lokality
•     důsledkem místních rizikových faktorů.

4. Závěr

Bezpečnost se tradičně určuje prostřednictvím ukazatelů nehodovosti. Existují však rozdílné ukazatele podávající rozdílné výsledky. Zaznamenané počty nehod jsou navíc zatíženy vlivem matoucích proměnných, především regresí k průměru.

Východiskem z této situace je modelování bezpečnosti, konkrétně očekávaného počtu nehod v závislosti nejen na intenzitě ale i na dalších parametrech. Výsledný predikční model nehodovosti poskytuje hodnoty očekávané četnosti nehod – ty jsou vhodnější než zaznamenaná četnost nehod, která je zatížena vlivem regrese k průměru, jak bylo prezentováno na dalším příkladu. Posledním krokem je kombinace zaznamenaných hodnot s predikovanými pomocí empirické Bayesovy metody.

Tento postup se může zdát nový a jistě potrvá, než se stane součástí české praxe. V zemích západní a severní Evropy nebo např. Spojených státech a dalších zemích jsou tyto principy známy již od 80. let minulého století a do praxe se dostávají postupně, plně aplikovány dosud nejsou. Může však najít uplatnění v mnoha úlohách řízení bezpečnosti, mezi něž patří:

• identifikace nehodových míst, jejich analýza a diagnóza,
• výběr a realizace opatření podle priorit,
• hodnocení účinnosti opatření.

Ve všech těchto úlohách se v české praxi v současnosti používá zaznamenaný počet nehod a z něj odvozená kritéria a ukazatele.

Zavedení do české praxe může zároveň podpořit aktuální transpozici evropské Směrnice o řízení bezpečnosti silničního provozu (viz aktuální přehled [6]): ta obsahuje, kromě známých postupů bezpečnostního auditu a bezpečnostní inspekce i dva postupy, které vyžadují kvantifikaci. Jedná se o „hodnocení dopadů na bezpečnost silničního provozu u projektů infrastruktury“ (road safety impact assessment) a „klasifikaci vybraných úseků silniční sítě a následné kontroly na místě“ (network safety management). Podle nedávného výstupu evropského projektu [7, str. 45] by network safety management měl být založen právě na predikčních modelech a empirické Bayesově metodě; podobně pro road safety impact assessment je dle zprávy [11, str. I] doporučována empirická Bayesova metoda.

Pro úplnost lze závěr ještě doplnit: bezpečnost, popisovaná v obou částech článku, byla kvantifikována prostřednictvím nehod, tj. přímých ukazatelů bezpečnosti. Alternativním řešením jsou nepřímé ukazatele bezpečnosti, které mají prokázaný vztah k přímým ukazatelům; mezi nepřímé ukazatele patří např. dopravní konflikty, pro které se aktuálně vyvíjí metodika sledování a vyhodnocení [2]. Američtí autoři [19] konstatují, že odhadování četností nehod (tj. přímých ukazatelů) a sledování „náhradních ukazatelů bezpečnosti“ (tj. nepřímých ukazatelů) představují dva základní směry měření bezpečnosti. Podle dosavadních zkušeností [2] má každý z těchto směrů svá omezení a žádný z nich není úplně soběstačný; budoucí potenciál tedy může být i v jejich vhodné kombinaci.

Článek byl zpracován za podpory projektu výzkumu a vývoje Ministerstva dopravy č. CG711-078-160 „Vývoj metodiky hodnocení účinnosti opatření ke zvýšení bezpečnosti provozu na pozemních komunikacích“ a projektu bezpečnostního výzkumu Ministerstva vnitra č. VG20112015013 „Identifikace a řešení kritických míst a úseků v síti pozemních komunikací, které svým uspořádáním stimulují nezákonné a nepřiměřené chování účastníků silničního provozu“Ministerstva vintra, Programu bezpečnostního výzkumu ČR v letech 2010-2015 (BVII/2-VS).

Reference
[1] Ambros, J. Dopravně inženýrská data v českém prostředí: analýza dostupnosti, rozsahu a použitelnosti. Silniční obzor, roč. 72 (2011), č. 7-8, s. 204-209.
[2] Ambros, J. Vývoj metodiky sledování a vyhodnocování dopravních konfliktů. Silniční obzor, roč. 72 (2011), t.č. v tisku.
[3] Andres, J. a kol. Metodika identifikace a řešení míst častých dopravních nehod. Centrum dopravního výzkumu, v.v.i., Brno, 2001. ISBN 80-902141-9-3.
[4] Brněnské komunikace a.s. Ročenky dopravy Brno 1999 – 2010.
[5] De Pauw, E., Daniels, S., Brijs, T., Hermans, E., Wets, G. The magnitude of the regression to the mean effect in traffic crashes. 24th ICTCT workshop, Varšava, 27. – 28. 10. 2011.
[6] Dont, M., Košťálová, J. Transpozice směrnice o řízení bezpečnosti silničního provozu. Silnice a železnice, roč. 6 (2011), č. 4, s. 59-60 (http://www.silnice-zeleznice.cz/clanek/transpozice-smernice-o-rizeni-bezpecnosti-silnicniho-provozu/).
[7] Elvik, R. Assessment and applicability of evaluation tools: Current practice in a sample of European countries and steps towards a state-of-the-art approach. RISMET Deliverables Nr 4 and 5, 2011 (http://rismet.swov.nl/Content/Report/Rismetdeliverable4and5.pdf).
[8] Elvik, R. The predictive validity of empirical Bayes estimates of road safety. Accident Analysis and Prevention, roč. 40 (2008), č. 6, s. 1964-1969.
[9] Hauer, E. Observational Before-After Studies in Road Safety: Estimating the Effect of Highway and Traffic Engineering Measures on Road Safety. Elsevier, Oxford, 1997. ISBN 0 08 043053 8.
[10] Hauer, E., Harwood, D.W., Council, F.M., Griffith, M.S. Estimating Safety by the Empirical Bayes Method: A Tutorial. Transportation Research Record, č. 1784 (2002), s. 126-131.
[11] Høye, A., Elvik, R., Sørensen, M. Effects of road safety measures: a summary for use in impact assessment. TØI Report 1157/2011, Oslo. ISBN 978-82-480-1248-1 (http://www.toi.no/getfile.php/Publikasjoner/T%D8I%20rapporter/2011/1157-2011/1157-summary.pdf).
[12] Kutz, M. (ed.). Handbook of Transportation Engineering. McGraw-Hill, New York, 2004. ISBN 0-07-139122-3.
[13] Nicholson, A. Accident count analysis: the classical and alternative approaches. Traffic Safety Theory & Research Methods, Session 2: Models for evaluation, SWOV, Amsterdam, 26. – 28. 4. 1988.
[14] Persaud, B., Lyon, C. Empirical Bayes before-after safety studies: Lessons learned from two decades of experience and future directions. Accident Analysis and Prevention, roč. 39 (2008), č. 3, s. 546-555.
[15] Pokorný, P., Striegler, R. Představení projektu IDEKO – Identifikace a návrh na odstranění kritických míst na komunikacích II. třídy v Jihomoravském kraji. Silniční obzor, roč. 72 (2011), t.č. v tisku.
[16] Sørensen, M., Elvik, R. Black Spot Management and Safety Analysis of Road Networks – Best Practice Guidelines and Implementation Steps. TØI Report 919/2007, Oslo. ISBN 978-82-480-0809-5 (http://www.toi.no/getfile.php/Publikasjoner/T%D8I%20rapporter/2007/919-2007/919-2007-nett.pdf).
[17] Šenk, P., Ambros, J. Odhad počtu dopravních nehod na nově budovaných okružních křižovatkách. 19. Silniční konference, Zlín, 11. – 12. 10. 2011, s. 153-156.
[18] Švanda, M., Brněnské komunikace a.s., Útvar dopravního inženýrství, e-mailová korespondence, 24. 10. 2011.
[19] Tarko, A., Songchitruksa, P. Measuring Roadway Safety. Road Safety on Four Continents, Varšava, 5. – 7. 11. 2005, s. 168-179.